Cómo funciona la compresión de imágenes JPEG
2021 / Matías Bergerman, Pablo González Leiro, Milagros Moutin
Este trabajo fue realizado para la materia 22.05 - Análisis de Señales y Sistemas Digitales, del Instituto Tecnológico de Buenos Aires.
Profesor: Ing. Daniel Jacoby.
Trabajo completo en formato PDF 🔗
Codificador JPEG programado usando Python 🔗
Índice 🔗
- Introducción
- Espacios y modelos de color
- Transformada Coseno Discreta - DCT
- Proceso de Cuantización
- Codificación Huffman
- Problemas con la compresión JPEG
- Bibliografía
Introducción 🔗
El estándar de compresión JPEG desarrollado por el Joint Photographic Experts Group en 1992 1 fue y sigue siendo uno de los esquemas de compresión de imágenes más utilizados a nivel mundial. A pesar de que nuevos estándares fueron desarrollados desde entonces cuyas prestaciones superan a las del JPEG original, este mantiene su popularidad.
JPEG es un algoritmo de compresión con pérdida (lossy) y aprovecha las características de la percepción visual humana como también propiedades estadísticas de las imágenes y diversas herramientas matemáticas. El ojo humano es más sensible a cambios en luminosidad o brillo que a cambios en tonalidad de color, además no es sensible ante frecuencias espaciales de color altas, es decir, a cambios rápidos de color en una distancia corta dentro de una imagen. Estas dos deficiencias de la visión permiten eliminar o reducir cierta información de una imagen de forma tal que el espacio requerido para almacenarla se minimice, a la vez que se preserva la forma en que es percibida por el ojo humano.
A pesar de que un archivo JPEG puede ser codificado de diversos modos, el más usual de estos es con codificación JFIF. Es por esto que el alcance de este trabajo se limita al estudio e implementación de este método de codificación. En la figura 1 se puede observar un diagrama en bloques demostrando los pasos que sigue el codificador. El procedimiento a seguir por el algoritmo se puede resumir en la siguiente serie de tareas:
-
La representación de los colores de la imagen es convertida al espacio \(YC_BC_R\), que consiste de un componente de luminancia (\(Y\)) que representa el brillo, y dos componentes de crominancia o chroma (\(C_B\) y \(C_R\)), que representan color. Esto permite aislar la luminosidad del color para que sean tratados por separado mediante una transformación fácil de implementar a partir del espacio RGB.
-
La resolución de los datos de crominancia se reduce, usualmente por un factor de 2 o 3. Esto refleja el hecho de que el ojo humano es menos sensible a detalles finos de color que a detalles finos de la luminosidad.
-
La imagen se divide en bloques de 8×8 píxeles, y para cada bloque individual, se aplica una transformada de coseno discreta (DCT por sus siglas en inglés discrete cosine transform) a cada uno de los componentes: \(Y\), \(C_B\), y \(C_R\). La DCT es similar a la transformada de Fourier ya que produce un espectro de frecuencia espacial, pero requiere un menor número de operaciones produciendo resultados similares en la calidad de la imagen. Se utiliza la DCT en lugar de la DST ya que se encontró que se necesita un menor número de coeficientes para las señales típicas.
-
La amplitud de los componentes frecuenciales son cuantizados. La visión humana es mucho más sensibles a pequeñas variaciones de color o brillo sobre grandes áreas que a las variaciones de alta frecuencia. Por lo tanto, la magnitud de los componentes de alta frecuencia son almacenados con una menor precisión que los componentes de baja frecuencia. Es posible modificar la calidad de la imagen que produce el codificador eligiendo cuánto reducir la resolución de los componentes frecuenciales.
-
Los coeficientes resultantes para cada bloque de 8×8 píxeles es comprimido sin pérdidas (lossless) usando una variante de codificación Huffman.
-
Por último, los datos son almacenados en un archivo binario junto con la información necesaria para decodificar la imagen, como las tablas utilizadas en el proceso de cuantización y compresión. Alternativamente los datos pueden ser transmitidos a otro dispositivo para su recepción.
Para la decodificación se sigue el proceso inverso, excepto por la cuantización ya que es irreversible. La resolución de los componentes chroma se puede recuperar parcialmente mediante un algoritmo de interpolación (por ejemplo nearest neighbour o bilinear interpolation).

Figura 1: Diagrama en bloques del algoritmo de codificación JPEG/JFIF.
Espacios y modelos de color 🔗
Un espacio de color consiste en un sistema para identificar colores que usualmente depende de un “modelo de color", aunque en algunos casos como el espacio Pantone no se utiliza un modelo. Cada color en un espacio basado en un modelo de color se puede interpretar como un punto dentro de un sistema de coordenadas, de forma tal que conociendo los valores de estas coordenadas es posible reconstruir el color en cuestión.
Espacio RGB 🔗
El ojo humano detecta colores mediante tres tipos de foto-receptores (conos) que tienen una distinta respuesta en frecuencia a la luz. Como se puede ver en la figura 2, los máximos de estas respuestas se alinean aproximadamente con los colores azul, verde y rojo (los colores primarios de la luz).

Figura 2: Espectro de los conos del ojo humano.
La mayoría de las pantallas digitales aprovechan este fenómeno para emular diferentes colores al estimular los foto-receptores del ojo humano de la misma forma en que serían estimulados por el color deseado. Para esto deben emitir luz roja, verde y azul en las proporciones adecuadas, razón por la cual nace la familia de espacios de color RGB dentro de la cual existen distintas variantes pero que generalmente siguen un mismo principio (por ejemplo sRGB o Adobe RGB). En la figura 3 se puede ver una representación tridimensional del espacio RGB, sobre el cual se interpreta a cada color como un punto dentro del cubo con sus tres coordenadas correspondientes. Dado que es la manera en que funcionan la mayoría de las pantallas, este es uno de los espacios de color más utilizados para imágenes digitales.

Figura 3: Representación tridimensional del espacio RGB.
Otros espacios de colores 🔗
En función de las necesidades de la aplicación, existen diversos otros espacios de color. Por ejemplo, el espacio CMYK (Cyan, Magenta, Yellow, Key - Cian, Magenta, Amarillo, Negro) refleja las características del proceso de impresión, al indicar la cantidad de cada tinta que se debe aplicar. A diferencia de RGB que representa una adición de color, el espacio CMYK representa una síntesis sustractiva de color. Otro ejemplo es el espacio HSB/HSL (Hue, Saturation, Brightness - Matiz, Saturación, Brillo) que se utiliza mayormente por artistas dado que es más natural considerar al color en términos de matiz y saturación que como una síntesis aditiva o sustractiva.
Transformación al espacio \(YC_BC_R\) 🔗
En la compresión JPEG el espacio de color utilizado es el \(YC_BC_R\) que consiste de un componente de luminancia (\(Y\)) que representa el brillo, y dos componentes de crominancia o chroma (\(C_B\) y \(C_R\)) que representan color. Esto permite aislar la luminosidad del color para que sean tratados por separado, ya que como fue dicho anteriormente, la sensibilidad del ojo humano es diferente para el color que para el brillo siendo mucho más sensible a este último. Este no se trata de un espacio de color absoluto, sino que es una forma de codificar información RGB, lo cual quiere decir que para poder representar un color \(YC_BC_R\) es necesario conocer el espacio de color RGB específico que se quiere utilizar (por ejemplo sRGB). La transformación entre el espacio RGB y \(YC_BC_R\) corresponde a una transformación lineal, aunque también es posible introducir alinealidades mediante una corrección gamma. Las ecuaciones correspondientes a esta transformación para valores no-signados de 8 bits son:
Los resultados de la conversión también son almacenados como datos no-signados de 8 bits, razón por la cual el resultado de cada ecuación debe ser limitado en el rango \([0, 255]\) y redondeado al entero más cercano.
En la figura 4 se puede ver el plano \(C_BC_R\) para un valor de luminancia constante de un medio. En este plano se puede apreciar que el punto central corresponde al color gris, el cual se asemejará al blanco o al negro en función del valor de luminancia, mientras que en los extremos de la escala se encuentran el rojo y el azul.

Figura 4: Plano Cb Cr para un valor de luminancia constante de un medio.
Submuestreo de crominancia 🔗
Luego de efectuar la transformación del espacio de color RGB al \(YC_BC_R\), el próximo paso del algoritmo es realizar un submuestreo de crominancia. Esto corresponde a reducir la resolución de los componentes \(C_B\) y \(C_R\) mientras que se preserva constante el componente \(Y\). Este es el primer punto en el cual se producen pérdidas de información de la imagen original, aunque para la mayor parte de los casos no representan un efecto significativo en la percepción de la imagen por el ojo humano dada su menor sensibilidad a cambios de color en comparación con el brillo.
El patrón de submuestreo normalmente se indica con una notación de tres dígitos separados por dos puntos J:a:b que describe el número de muestras de luminancia y crominancia en una región de J píxeles de ancho y 2 píxeles de alto. El significado de esta notación, de izquierda a derecha es el siguiente:
-
J: Referencia de muestreo de luminancia horizontal (ancho) que usualmente tiene un valor de 4.
-
a: Número de muestras de crominancia (\(C_B\) y \(C_R\)) en la primera fila de \(J\) píxeles.
-
b: Número de cambios de muestras de crominancia (\(C_B\) y \(C_R\)) entre la primer y segunda fila de \(J\) píxeles. El valor de \(b\) debe ser 0 o igual a \(a\) (excepto por ciertos casos irregulares).
En este trabajo, el patrón de submuestreo elegido es el 4:2:0 dado que es uno de los más utilizados. Este corresponde a una reducción a la mitad de tanto la resolución horizontal como vertical. En la figura 5 se ponen en evidencia los efectos del submuestreo en una imagen digital. La amplitud de los componentes de crominancia se muestran en escala de grises para que puedan ser mejor apreciados.
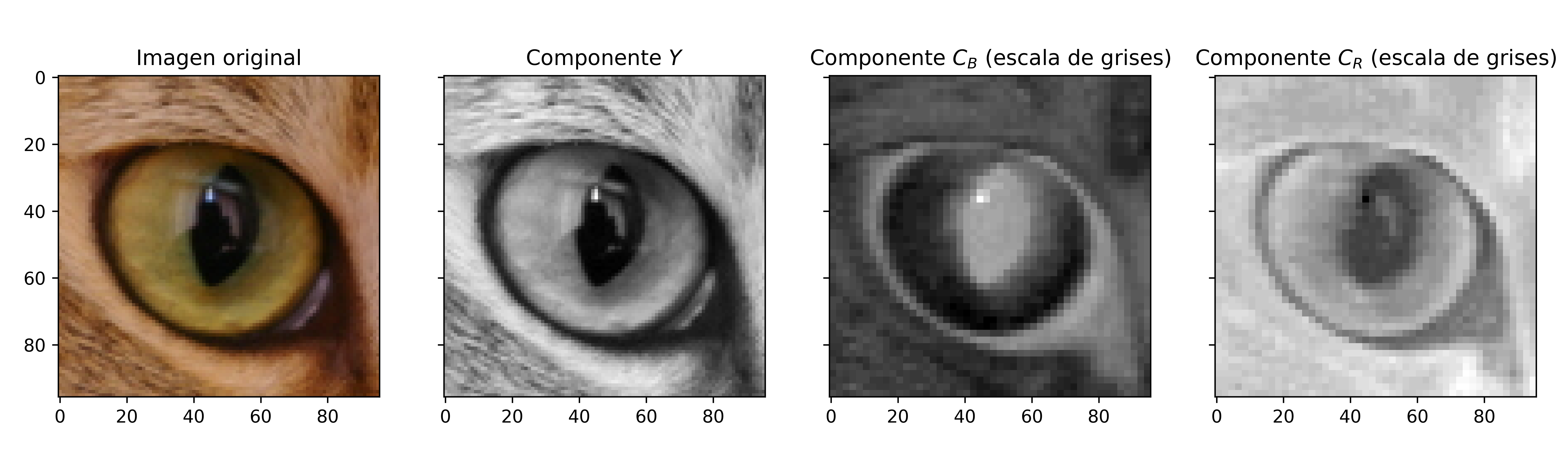
Figura 5: Efectos del submuestreo de crominancia en una imagen.
En JPEG/JFIF, como también H.261 y MPEG-1, se suelen tomar muestras ubicadas de forma intersticial, entre medio de las muestras de luminancia. Dado que se parte de una imagen digital con una resolución definida, este submuestreo se puede realizar en forma sencilla dividiendo los componentes \(C_B\) y \(C_R\) de la imagen en bloques de 2x2, y tomando el promedio de cada uno de estos bloques como la nueva muestra de la imagen submuestreada.
Transformada Coseno Discreta - DCT 🔗
El objetivo de esta sección es tomar los bloques de dimensión 8x8 y descomponer esta información en distintas bandas de frecuencia. A continuación veremos como se define la DCT y por qué es de importancia en este proceso.
Introducción 🔗
Una transformada matemática es una función \(A(k)\) cuyo dominio son las funciones discretas \(x(n)\) y se define:
$$A(k) = \sum_{n=0}^{N-1} x(n) \phi_{k}^{*}(n)$$
Siendo \(N\) el período
de la función \(x(n)\) y donde el conjunto de las funciones \(\phi_{k}(n)\),
con \(0\leq n\leq N-1\) es una base ortogonal.
A su vez, la función \(x(n)\) en el intervalo entre \(0 \leq n \leq N-1\) se
puede escribir como combinación lineal de la base ortogonal formada por
los \(\phi_{k}(n)\), donde los coeficientes lineales se forman con los
valores de la transformada \(A(k)\) de la siguiente forma:
$$x(n) = \frac{1}{N}\sum_{k=0}^{N-1} A(k) \phi_{k}(n)$$
Para definir la
Transformada Discreta de Fourier, se propuso que la base ortogonal sean
las funciones del tipo \(e^{\frac{j2\pi kn}{N}}\). Con esta definición,
aunque la función x(n) sea real, los valores de la transformada A(k)
serán complejos. Sin embargo, se puede definir una base ortogonal, por
ejemplo formada por funciones del tipo \(cos(\omega t + \phi )\), de forma
que los valores de la transformada \(A(k)\) sean reales cuando la función
\(x(n)\) sea real.
A partir de este concepto se construye la Transformada Coseno Discreta,
usando una base ortogonal del tipo cosenoidal, que presenta ciertas
propiedades que la hacen muy útil para varias aplicaciones relacionadas
con el procesamiento de imágenes y sonido. En lo que refiere a
compresión JPEG, sucede que la base ortogonal cosenoidal funciona como
una base de imágenes a partir de la cuales podemos descomponer la imagen
que queremos comprimir, como una combinación lineal de las imágenes
base.
Definición 🔗
Los desarrollos matemáticos y ejemplos que se muestran en esta sección fueron obtenidos del libro Discrete-Time Signal Processing del autor A. V. Oppenheim que se está citado en la bibliografía.
La base ortogonal para la DCT serán funciones cosenoidales, que tienen la propiedad de ser periódicas y pares. Por lo tanto, cualquier combinación lineal de funciones pares, será par. Es decir que se asume que la función a descomponer \(x(n)\) fuera del rango \(0\leq n\leq N-1\) debe presentar simetría par y ser periódica. Existe un total de ocho formas de extender la función \(x(n)\) fuera del rango tal que la función \(x(n)\) tenga periodicidad y simetría par, que dan origen a múltiples definiciones para la transformada. De estas definiciones mostraremos la más comunes, llamadas DCT-I y DCT-II, para focalizarnos luego en DCT-II, que será la que usaremos en el proceso de compresión.
DCT-I 🔗
Supongamos que se tiene la secuencia \(x(n)\) que muestra la figura 6, la cual se quiere extender fuera del período \(0\leq n\leq N-1\).
Figura 6: Función discreta x(n) a extender.
Podemos extender \(x(n)\) según como muestra la figura 7 y formar la función extendida de \(x(n)\), \(x_{1}(n)\).
Figura 7: x1(n), extensión de x(n).
Esta función tiene un período igual a \(2N-2\). Notar que tiene simetría par respecto de cualquier \(n\) tal que sea múltiplo de \((N-1)\) y \(n = 0\). Si queremos escribir cuanto vale la función \(x_{1}(n)\) como sumas de \(x(n)\) desplazadas, tenemos que notar que para los \(n = k\cdot (N-1)\), con \(k \in \mathbb{Z}\), los valores de la función se van a solapar. Es por esto que define la función \(x_{\alpha}(n)\):
$$x_{\alpha}(n) = \begin{cases} \frac{1}{2}\cdot x(n) & \quad \text{si } n = 0\text{ o } n = N-1\\ x(n) & \quad \text{si no} \end{cases}$$
Entonces, se escribe la función \(x_{1}(n)\) en función de \(x_{\alpha}\) de la siguiente forma:
$$x_{1}(n) = x_{\alpha}(n)_{2N-2} + x_{\alpha}(-n)_{2N-2}$$
Tomando a \(x_{\alpha}(n)_{2N-2}\) y \(x_{\alpha}(-n)_{2N-2}\) como funciones que
repiten la función \(x_{\alpha}\) para cada \(n\) múltiplos de \(2N-2\). Notar
que para \(n=0\) y \(n=N-1\) están definidas ambas funciones
\(x_{\alpha}(n)_{2N-2}\) y \(x_{\alpha}(-n)_{2N-2}\), pero al sumarlas se
promedia el valor de ambas.
A partir de esta extensión de \(x(n)\) se define la DCT-I como:
$$X^{C1}(k) = 2 \sum_{n=0}^{N-1} \alpha(n)x(n) cos\left (\frac{\pi kn}{N-1} \right )$$
con \(k = 0,..., N-1\).
Otra forma equivalente para expresarla sería:
$$X^{C1}(k) = \frac{1}{2}\cdot (x_{0} + (-1)^{k}x(n)) + \sum_{j = 1}^{N-2} cos\left ( \frac{\pi jk}{N-1} \right )$$
con \(k = 0,..., N-1\).
Fuera del intervalo \(k= 0,...,N-1\), la función será equivalente la
extensión \(x_{1}(n).\) Por último, la función \(x(n)\) puede escribirse
como combinación lineal de la base ortogonal formada por el siguiente
conjunto de
funciones:
$$\left \{cos\left ( \frac{\pi kn}{N-1}\right )\right \} \text{ con } k=0,..,N-1$$
de la siguiente forma:
$$x(n) = \frac{1}{N-1} \sum_{k = 0}^{N-1} \alpha(k) X^{C1}(k)cos\left ( \frac{\pi kn}{N-1} \right )$$
DCT-II 🔗
Supongamos que se tiene nuevamente la misma función \(x(n)\), pero se la quiere extender de forma distinta a como se extendió \(x_{1}(n)\) en la sección anterior, manteniendo la condición de que la función extendida tiene que ser una función par con respecto a \(n=0\) y periódica. Se propone la extensión que llamamos \(x_{2}(n)\) y se muestra en la Figura 8.
Figura 8: x2(n), extensión de x(n).
Inspeccionando la Figura 8 en comparación a 7, vemos que ya no tenemos simetría par en los \(n\) múltiplos de \(n = N+1\), salvo en \(n = 0\). La simetría se encuentra respecto del puntos medio entre \(N + 1\) y \(N\), pero al ser la extensión una función discreta este punto no se encuentra en el dominio. El período de la función \(x_{2}(n)\) es \(2N\), y podemos expresar la función \(x_{2}(n)\) como función de \(x(n)\) de la siguiente forma:
$$x_{2}(n) = x(n)_{2N} + x(-n-1)_{2N}$$
A partir de la extensión \(x_{2}(n)\) de \(x(n)\) se define la DCT-II como:
$$X^{C2}(k) = 2\sum_{n=0}^{N-1}x(n)cos\left ( \frac{\pi k(2n + 1)}{2N}\right ) \label{eq:DCT2-NoUni}$$
(9)
con k = 0,..., N-1. La función \(x(n)\) puede escribirse como combinación lineal de la base ortogonal formada por el siguiente conjunto de funciones:
$$\left \{cos\left ( \frac{\pi k(2n+1)}{2N}\right )\right \} \text{ con } k=0,..,N-1$$
de la siguiente forma:
$$x(n) = \frac{1}{N} \sum_{k=0}^{N-1} \beta(k)X^{C2}(k)cos\left ( \frac{\pi k(2n+1)}{2N} \right )$$
con \(k=0,...,N-1\) y definiendo la función \(\beta (k)\) de la siguiente forma:
$$\beta(k) = \begin{cases} \frac{1}{2} & \quad \text{si } k = 0\\ 1 & \quad 1\leq k\leq N-1 \end{cases}$$
Como comentario final para esta sección, en ciertas ocasiones se requiere incluir los llamados “factores de normalización" que hacen unitaria a la transformada, es decir que su base sea ortonormal y además se cumpla la siguiente propiedad:
$$\sum_{n=0}^{N-1}x(n)^2 = \sum_{k =0}^{N-1}X^{C2}(k)^2$$
Lo que se hará es simplemente redistribuir los factores de normalización entre la transformada y su inversión. Por lo tanto, otra definición para la transformada y su inversa que se pueden encontrar frecuentemente son las siguientes:
$$\tilde{X^{C2}} = \sqrt{\frac{2}{N}}\tilde{\beta}(k)\sum_{n=0}^{N-1}x(n)\cdot cos\left ( \frac{\pi k(2n + 1)}{2N}\right )$$ $$x(n)= \sqrt{\frac{2}{N}}\sum_{n=0}^{N-1}\tilde{\beta}(k)\tilde{X^{C2}} cos\left ( \frac{\pi k(2n + 1)}{2N}\right )$$
con \(0\leq k\leq N-1\) y definiendo \(\tilde{\beta}(k)\) de la siguiente forma:
$$\tilde{\beta}(k) = \begin{cases} \frac{1}{\sqrt{2}}& \quad \text{si } k = 0\\ 1 & \quad k=1,2,...,N-1 \end{cases}$$
Definición Multidimensional 🔗
Anteriormente se definió a la transformada cuyo dominio son las
funciones \(x:\mathbb{N}\rightarrow \mathbb{R}\). En nuestra aplicación se
quiere buscar la transformada de funciones del tipo
\(x:\mathbb{N}^2\rightarrow \mathbb{R}\).
Para esto se define la transformada bidimensional DCT-II unitaria que
consiste en hacer la transformada primero en una dimensión y luego de la
otra de la siguiente forma:
$$X_{ij} = \frac{\tilde{\beta}(i)\tilde{\beta}(j)}{\sqrt{NM}}\sum_{n = 0}^{N-1}\left [\sum_{m = 0}^{M-1} x(n,m) cos\left ( \frac{\pi i (2m+1)}{2M} \right ) \right ] cos \left ( \frac{\pi j (2n+1)}{2N} \right )$$
Si bien esta es la definición formal de la transformadas multidimensional, más adelante en el análisis matricial se presentará otra forma más simplificada de poder calcularla.
Representación matricial para DCT 🔗
En la aplicación de compresión JPEG, se busca calcular la transformada
DCT-II bidimensional unitaria, donde se conoce de antemano que la
entrada es siempre una matriz cuyas dimensiones son 8x8. Para hacer este
cálculo de forma computacional, optamos por obtener una representación
matricial de la transformada. Es por esto que se plantea un análisis
matricial para obtener la DCT-II unidimensional a partir del cual se
simplifica el cálculo de la transformada bidimensional.
Siendo que se desea calcular una transformada lineal y discreta, para
una entrada \(x(n)\) de periodo N, existe una matriz de dimensión \(NxN\)
tal que nos permite calcular la transformada X de la siguiente forma:
$$X = C_{N}x$$
Siendo \(X_{Nx1}\) los valores que toma la DCT y \(x_{Nx1}\) los valores que toma la función x(n) de entrada. La matriz \(C_{N}\) se puede obtener teniendo en cuenta la definición de transformada bidimensional presente en la sección previa. De esta forma, obtener la transformada coseno inversa es simplemente:
$$x = C_{N}^{-1}X$$
Como la base de la transformación cosenoidal es ortogonal, la matriz \(C_{N}\) cumplirá la siguiente propiedad:
$$C_{N}^{-1} = C_{N}^{T}$$
Este
propiedad facilita en gran medida el cálculo de la antitransformada.
Si se desea calcular una transformada bidireccional para una entrada
\(x(i,j)\), de dimensión \(NxM\), basta con calcular:
$$X = C_{N}xC_{M}$$
Si sucede que la dimensión de entrada es \(NxN\) (el caso de la aplicación en cuestión), se cumple lo siguiente:
$$X_{NxN} = C_{N}xC_{N}^{T} \label{eq:dtc_matricial}$$
(17)
De la misma forma, podemos la entrada x(n) de la siguiente forma: \(x = C_{N}^{T}XC_{N} %\label{eq:dtc_matricial}\) Además, para una transformada DTC-II unitaria se tiene que esta matriz vale lo siguiente:
$$C_{k,n}= \left\{ \begin{array}{lcc} \frac{1}{\sqrt{N}} & si & k = 0,\;\; 0 \leq k\leq N-1 \\ \\\sqrt{\frac{2}{N}} \cdot cos\left ( \frac{\pi (2n+1)k }{2N}\right )& si & 1\leq k\leq N,\;\; 0\leq n\leq N-1 \\ \end{array} \right.$$
Siendo que se van a computar matrices de dimensión 8x8, se pueden determinar los valores de la matriz y su traspuesta de antemano en el código y con la entrada se aplica la fórmula 17 y se obtiene así la DCT. Esta matriz que llamamos “Matriz Base" se observa a continuación y se representa en la Figura 10.
$$ \begin{bmatrix} 0.354 & 0.354 & 0.354 & 0.354 & 0.354 & 0.354 & 0.354 & 0.354\\ 0.49 & 0.416 & 0.278 & 0.098 & -0.098 & -0.278 & -0.416 & -0.49\\ 0.462 & 0.191 & -0.191 & -0.462 & -0.462 & -0.191 & 0.191 & 0.462\\ 0.416 & -0.098 & -0.49 & -0.278 & 0.278 & 0.49 & 0.098 & -0.416\\ 0.354 & -0.354 & -0.354 & 0.354 & 0.354 & -0.354 & -0.354 & 0.354\\ 0.278 & -0.49 & 0.098 & 0.416 & -0.416 & -0.098 & 0.49 & -0.278\\ 0.191 & -0.462 & 0.462 & -0.191 & -0.191 & 0.462 & -0.462 & 0.191\\ 0.098 & -0.278 & 0.416 & -0.49 & 0.49 & -0.416 & 0.278 & -0.098\\ \end{bmatrix} $$
Figura 9: Coeficientes de la matriz base DCT.

Figura 10: Matriz Base de la DCT.
A continuación ampliaremos sobre las propiedades de la DCT, pero en particular sobre la DCT-II ya que es la trasformación utilizada por los algoritmos de compresión.
Comportamiento en Alta Frecuencia 🔗
A continuación se amplia sobre la principal propiedad de la DCT,
focalizando en particular sobre la DCT-II normalizada ya que es la
trasformación utilizada por los algoritmos de compresión.
Tomando como ejemplo la secuencia que se muestra en la Figura
11
se busca extenderla de la forma que se extiende en DFT y DCT-II.
Figura 11: Secuencia discreta a extender x(n).
A continuación, en la figura 12 se muestra cómo serían las extensiones de x(n) para la DFT y DCT respectivamente.
Figura 12: Extensiones de x(n) para DFT y DCT-II respectivamente.
Comparando las dos extensiones, se puede ver que la extensión para
DCT-II presenta menos discontinuidades que DFT, ergo, tiene menores
componentes a alta frecuencia. Decir que la señal presentará menos
componentes a alta frecuencia equivale a decir que para la transformada
\(X\) los coeficientes de menor orden son mucho más altos que aquellos de
mayor orden (observando la matriz transformada \(X\), los coeficientes de
arriba a la izquierda resultan ser de mayor valor que aquellos de abajo
a la derecha). Pensando ahora en cómo sería la matriz que representa la
DFT, no sucedería lo mismo ya que al extender estamos agregando
componentes de alta frecuencia. Esto permite comprimir la información en
una menor cantidad de coeficientes, y así poder descartar los
coeficientes de mayor frecuencia.
Otra forma de verlo sería pensar que la energía de la señal viene dada
por la sumatoria del módulo al cuadrado de los \(X_{ij}\). Entonces, la
mayor cantidad de energía está concentrada en los primeros coeficientes
teniendo en cuenta la propiedad que tiene la matriz \(X\), cosa que no
sucede con la DFT cuya energía se encuentra más equitativamente
distribuida.
A esta propiedad se la conoce como Energy Compaction, y dice que
usando la DCT por sobre la DFT se puede comprimir la misma información
en una menor cantidad de coeficientes. Si se quieren descartar los
coeficientes de alta frecuencia utilizando DFT, se pierde mucha
información, lo que lleva a distorsión. Utilizando la DCT se los pueden
descartar ya que la misma información se encuentra compactada en los
coeficientes de baja frecuencia.
Fast Cosine Transform - FCT 🔗
A continuación se presenta un método mediante el cual, usando el algoritmo de Fast Fourier Transform se puede implementar un algoritmo para calcular la DCT donde se pase de una complejidad \(\Theta (n) = N^2\) para la forma de cálculo que mostramos anteriormente a uno cuyo orden sea \(\Theta (n) = N\cdot log_{2}N\). Esta idea se tratada en el trabajo escrito por J. Makhould que fue publicado en febrero de 1980 y se encuentra citado en la bibliografía. La idea central es que a partir de la relación entre la DCT y la DFT se puede primero buscar la Transformada de Fourier usando el algoritmo FFT y luego usar la relación que encontremos entre la DCT y la DFT.
Relación DCT-DFT 🔗
La DCT puede ser considerada esencialmente una DFT de una extensión par de una señal. Es decir, supongamos que se quiere encontrar la DCT una secuencia real x(n) (\(0\leq n\leq N-1\)), esta deriva de la DFT de una secuencia de extensión par 2N y(n) de la siguiente forma:
$$y(n)= \left\{ \begin{array}{lcc} x(n) & & 0 \leq n \leq N-1 \\ \\ x(2N-n-1) & & N < n < 2N-1 \\ \end{array} \right.$$
Ahora, se busca la DFT de y(n):
$$Y(k) = \sum_{n=0}^{2N-1} y(n)\cdot W_{2N}^{nk}$$
Siendo la base ortogonal \(W_{M} = e^{-j2\pi /M}\):
$$Y(k) = \sum_{n=0}^{N-1}x(n)\cdot W_{2N}^{nk} + \sum_{n=N}^{2N-1}x(2N-n-1)\cdot W_{2N}^{nk}$$
Se puede reescribir esta última expresión de la siguiente forma:
$$y(k) = W_{2N}^{-\frac{k}{2}} \cdot 2\sum_{n=0}^{N-1}x(n)\cdot cos\left ( \frac{\pi(2n+1)k}{2N} \right )$$
Ahora, teniendo en mente la definición de DCT-II que muestra la fórmula 9, se puede escribir la siguiente relación entre la DFT y la DCT:
$$Y(k) = W_{2N}^{-\frac{k}{2}}C(k)$$
Siendo \(C(k)\) la DCT. Por lo tanto, la DCT de x(n) puede computarse tomando la
DFT la función y(n) de período 2N y multiplicando el resultado por
\(W_{2N}^{\frac{k}{2}}\).
Otra forma de obtener la DCT en función de la DFT sería:
$$C(k) = 2\; Re \; \left [ W_{2N}^{\frac{k}{2}}\sum_{n=0}^{N-1} x(n)\; W_{2N}^{nk}\right ]$$
Es decir que se puede obtener la DCT tomando 2N puntos de la secuencia original x(n) y utilizando esta fórmula.
Proceso de Cuantización 🔗
Hasta ahora, todos los pasos a seguir en el proceso de compresión fueron reversibles (excepto el submuestreo); es decir que no hubo significativas pérdidas de información. Es en el proceso de cuantización donde inevitablemente se degradará la calidad de la imagen. Sin embargo, esta pérdida puede ser tal que sea imperceptible o mínima según un criterio específico que se asigna. A continuación se examinará en más detalle como se lleva a cabo proceso de cuantización, como se define la llamada Matriz de Cuantificación y qué error se introduce en el proceso.
La cuantización se aplicará a la salida de la DCT. Es decir que se busca cuantizar matrices de dimensión 8x8. Esto consiste en dividir cada uno de los valores de la DCT por los valores que presentan en la llamada Matriz de Cuantificación. Esta es una matriz de dimensión 8x8 que presenta en la fila \(i\) y columna \(j\) como se cuantificará el coeficiente \(C_{ij}\) correspondiente a la transformada coseno. Finalmente se toman todos valores enteros, con lo cual se debe redondear al entero más cercano:
$$B_{ij} = \text{round}\left ( \frac{C_{ij}}{Q_{ij}} \right )$$
Siendo \(B\) la matriz cuantizada, \(C\) la matriz DCT y \(Q\) la tabla o matriz de cuantización.
Si bien los valores de la matriz se determinan de forma empírica, existen algunos criterios a utilizar. Igualmente, cada cámara de fotos, software de compresión, etc, define sus propias matrices; es decir que los valores no responden a un criterio matemático, sino más bien subjetivo y práctico del fabricante. Podemos decir que el principal criterio es la calidad de imagen que se busca. A menor calidad de imagen, mayor será el valor por el que habrá que dividir la salida del DCT y más posibilidades hay de que al hacer la división, el resultado sea un número menor que al redondear se transforme en cero. Si el resultado fuera una matriz con todos unos, eso significaría que se tiene la calidad más alta posible. Aun así, siendo que la salida de la DCT es una matriz de números que muy probablemente no sean enteros y que el resultado de la división se redondea, siempre se pierde algo de información.
Por otro lado, teniendo en cuenta que a la salida de la DCT se tiene el contenido de la señal divido en diferentes bandas de frecuencia, según los números que se eligen para la matriz se pueden descartar distintas bandas de frecuencias. Es mediante este control de calidad que se pueden eliminar las componentes de alta frecuencias ya que, recordando que la DCT comprime la información de la imagen en las frecuencias más bajas, podemos despreciar los valores de las componentes en alta frecuencias. Además, descartar los valores de alta frecuencia tiene sentido ya el ojo humano es mucho más sensible a las bajas frecuencias que a la altas, entonces la matriz de cuantización tendrá valores típicamente mayores abajo a la derecha que arriba a la izquierda.
Tablas de Cuantización 🔗
El estándar JPEG define las tablas de cuantización que se muestran en la Figura 13 teniendo en una cuenta que la matriz a cuantificar es una DCT-II normalizada.
Figura 13: Tablas de cuantificación para Luminancia y Crominancia respectivamente.
Estas tablas representan lo que el estándar define como un 50% de calidad. Si las tablas estuvieran compuestas exclusivamente por números 1, entonces no habría reducción de precisión y la calidad sería del 100%. En las figuras 14, 15 y 16 se muestra una imagen comprimida mediante el algoritmo JPEG usando submuestreo 4:2:0 con tablas de calidad 100% y 50% respectivamente, donde se observa que a menor calidad los detalles finos de las texturas se ven deteriorados, pero a gran escala estas diferencias son poco perceptibles.

Figura 14: Imagen digital original.

Figura 15: Imagen comprimida mediante JPEG con calidad 100%.

Figura 16: Imagen comprimida mediante JPEG con calidad 50%.
Codificación Huffman 🔗
Para comprimir el tamaño del archivo, se codificarán los bloques usando
codificación Huffman. Para ello se cuenta con cuatro tablas, ya que se
usan tablas distintas para codificar la parte DC y la parte AC de las
componentes de luminosidad y color.
El algoritmo para generar estos códigos nos permite maximizar la
entropía, al asignar códigos más cortos para codificar situaciones más
probables. El diagrama de la figura
17 esquematiza la lógica para generar el
código de un bloque de 8x8 píxeles.
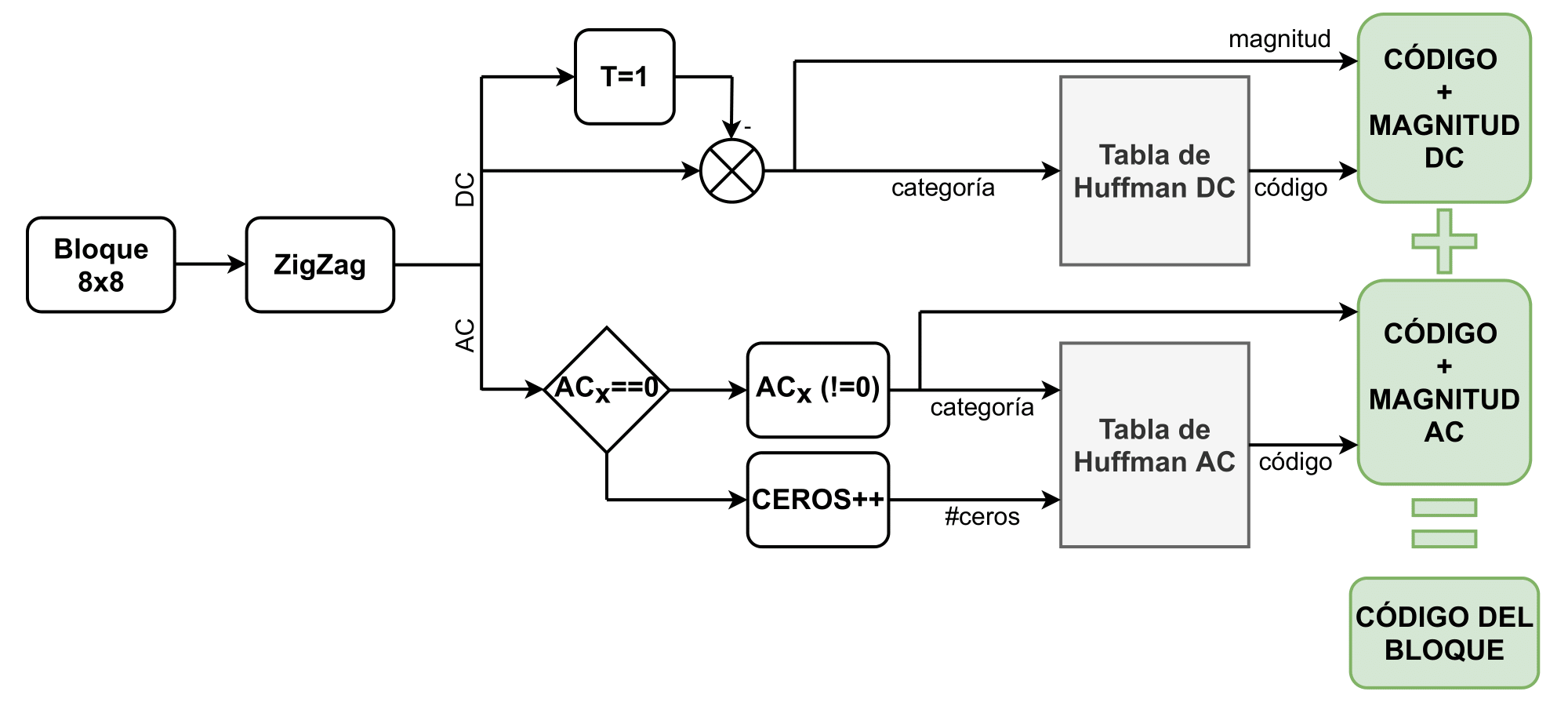
Figura 17: Diagrama de la codificación Huffman de un bloque
Difference encoding, Running length encoding y Códigos de Huffman 🔗
Para la parte DC, se aplica difference encoding, es decir que se guarda la diferencia de la componente de continua con respecto al bloque anterior. Así es más común tener valores chicos para estas diferencias, que serán codificados con códigos más cortos. Un código de cada tabla DC da la categoría del valor codificado. La categoría es el mínimo número de bits necesario para codificarlo, usando complemento a uno (ver las distintas categorías con sus rangos de valores correspondientes en la tabla 1). Por ejemplo, el valor -10 es categoría 4, por lo que se representa con 4 bits, 0b0101 (ya que 10 = 0b1010). Las tablas DC tienen códigos para las categorías 0-11, siendo 0 la categoría correspondiente a la magnitud cero. A modo de ejemplo la tabla 2 corresponde a la tabla DC para la luminosidad.
| Rango | Categoría |
|---|---|
| 0 | 0 |
| -1,+1 | 1 |
| -3,-2,+2,+3 | 2 |
| -7,...,-4, +4,...,+7 | 3 |
| -15,...,-8,+8,...,+15 | 4 |
| -31,...,-16,+16,...,+31 | 5 |
| -63,...,-32,+32,...,+63 | 6 |
| -127,...,-64,+64,...,+127 | 7 |
| -255,...,-128,+128,...,+255 | 8 |
| -511,...,-256,+256,...,+511 | 9 |
| -1023,...,-512,+512,...,+1023 | 10 |
| -2047,...,-1024,+1024,...,+2047 | 11 |
Tabla 1: Categorías para distintos rangos de valores. En este trabajo se usa hasta categoría 11.
| Categoría de la diferencia DC | Código binario |
|---|---|
| 0 | 00 |
| 1 | 010 |
| 2 | 011 |
| 3 | 100 |
| 4 | 101 |
| 5 | 110 |
| 6 | 1110 |
| 7 | 11110 |
| 8 | 111110 |
| 9 | 1111110 |
| 10 | 1111110 |
| 11 | 111111110 |
Tabla 2: Tabla de Huffman para la componente continua de la luminosidad.
Para la parte de AC es común que tras la cuantización se anulen las componentes de alta frecuencia, de forma que al aplicar el zigzag quedan muchos ceros consecutivos. Para aprovechar esto se ordenan los elementos de cada bloque en un vector según lo indica la figura 18 y se aplica running length enconding, esto es, se codifica la cantidad de ceros con el valor no nulo que los sucede. Por ejemplo, hay 9 ceros y luego el valor 3, se codifica para la cantidad de ceros 9 y la categoría 2 (3=0b11) con el código 0b1111111110111111. Después del código va la magnitud 0b11. La tabla AC tiene códigos para contar entre 0 y 15 ceros seguidos por una magnitud de categoría 1 a 10. Además hay un código para indicar la terminación de un bloque y otro para colocar 16 ceros sin magnitud en el caso de tener más de 15 ceros consecutivos. Esto da un total de 162 códigos. Las tablas usadas se pueden ver en el código adjunto.

Figura 18: Recorrido en zigzag para vectorizar un bloque de 8x8.
Entrelazamiento (Interleaving) 🔗
Para hacer posible la decompresión para distintos tipos de sistemas, es necesario que las componentes de la imagen se guarden intercaladas. Para ello cada componente se divide en regiones rectangulares de \(H_i\times V_i\) bloques; donde \(H_i\) y \(V_i\) son los factores de muestreo en la direcciones horizontal y vertical, respectivamente. Tanto las regiones de cada componente como los bloques dentro de una región, se ordenan de izquierda a derecha y de arriba a abajo. Se define el término MCU (Minimum Coded Unit) para referirse al grupo más chico de bloques intercalados. En la figura 19 se puede ver esta para una imagen de 48x32 píxeles (6x4 bloques), donde los componentes de crominancia fueron submuestrados con patrón 4:2:0.
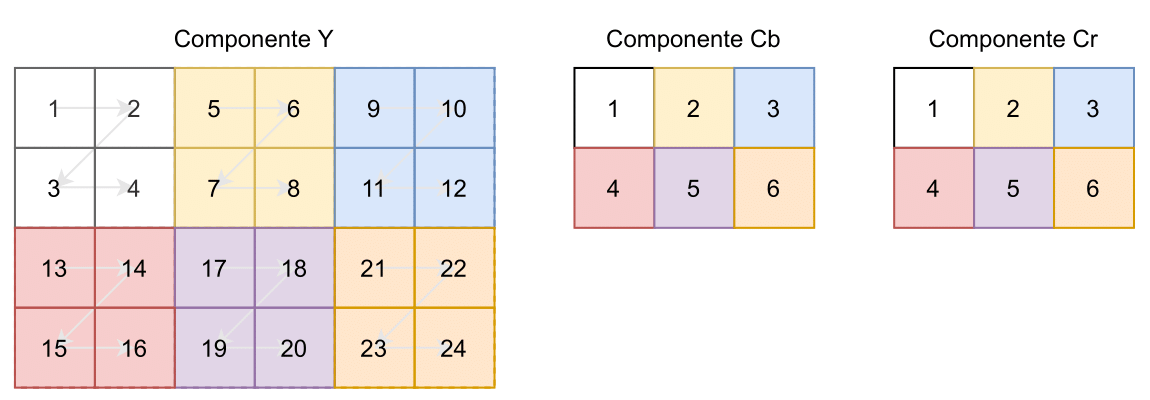
Figura 19: Ejemplo de intercalación de los componentes de la imagen.
Las MCUs son los siguientes, donde \(Y_i\) indica el i-ésimo bloque de la luminancia y \({C_R}_i\) y \({C_B}_i\) hacen lo propio con la crominancia. El máximo admisible de bloques por MCU es 10, en este caso son 6.
| $$MCU_1:$$ | $$Y_1$$ | $$Y_2$$ | $$Y_3$$ | $$Y_4$$ | $${C_B}_1$$ | $${C_R}_1$$ |
| $$MCU_2:$$ | $$Y_5$$ | $$Y_6$$ | $$Y_7$$ | $$Y_8$$ | $${C_B}_2$$ | $${C_R}_2$$ |
| $$MCU_3:$$ | $$Y_9$$ | $$Y_{10}$$ | $$Y_{11}$$ | $$Y_{12}$$ | $${C_B}_3$$ | $${C_R}_3$$ |
| $$MCU_4:$$ | $$Y_{13}$$ | $$Y_{14}$$ | $$Y_{15}$$ | $$Y_{16}$$ | $${C_B}_4$$ | $${C_R}_4$$ |
| $$MCU_5:$$ | $$Y_{17}$$ | $$Y_{18}$$ | $$Y_{19}$$ | $$Y_{20}$$ | $${C_B}_5$$ | $${C_R}_5$$ |
| $$MCU_6:$$ | $$Y_{21}$$ | $$Y_{22}$$ | $$Y_{23}$$ | $$Y_{24}$$ | $${C_B}_6$$ | $${C_R}_6$$ |
El código que representa a toda la imagen es la concatenación de las secuencias binarias de cada MCU, que a su vez es una concatenación de 6 bloques. Se agregan 1s al final para completar el último byte si corresponde.
Rellenado de bytes (Byte stuffing) 🔗
Para evitar que se detecte un \(0xFF\) como el inicio de un marcador, se utiliza byte stuffing agregando luego de todo \(0xFF\) presente dentro de los datos de la imagen, un byte \(0x00\). Así al leer el archivo, si se lee \(0xFF00\) se entiende que es parte de los bits de datos de la imagen y que debe omitirse el byte \(0x00\) ya que fue agregado para evitar esta ambigüedad.
Problemas con la compresión JPEG 🔗
Para realizar la compresión JPEG de forma tal que el resultado sea perceptiblemente muy similar a la imagen original se deben cumplir ciertas condiciones. En particular, la imagen no debe tener componentes de frecuencia espacial demasiado altos, como por ejemplo cambios repentinos de color o luminancia. Dicha condición se cumple para la mayoría de las imágenes tomadas mediante una cámara de fotos del mundo físico, produciendo muy buenos resultados en imágenes naturales, sin embargo para imágenes generadas por computadora que contienen bordes nítidos o texto rasterizado no se verifica la condición mencionada. En este tipo de imágenes se producen “artefactos de compresión" que consisten generalmente de puntos o zonas de ruido al rededor del texto y los bordes nítidos. Este tipo de artefacto de compresión se denomina “ruido de mosquito", ya que se parece a un enjambre de mosquitos volando alrededor del objeto.
En la figura 20 se puede ver una imagen rasterizada del escudo del Instituto Tecnológico de Buenos Aires, mientras que en la figura 21 se muestra el resultado de comprimir la imagen mediante JPEG. En este caso, a pesar de que no se verifican las condiciones ideales para la compresión el resultado sigue siendo aceptable. Sin embargo, como se muestra en las figuras 22 y 23 al ampliar las imágenes los artefactos de compresión se vuelven evidentes.

Figura 20: Imagen rasterizada del escudo del ITBA.

Figura 21: Imagen del escudo del ITBA comprimida mediante JPEG con calidad 50%.

Figura 22: Imagen rasterizada del escudo del ITBA (ampliada).

Figura 23: Imagen del escudo del ITBA comprimida mediante JPEG con calidad 50% (ampliada).
Bibliografía 🔗
Libros: 🔗
-
A. V. Oppenheim, R. W. Schaffer and J. R. Buck, Discrete-Time Signal Processing, second ed. Upper Saddle River, New Jersey, US: Prentice Hall, 1999, pp 589-599.
-
J. G. Proakis and D. G. Manolakis, Signal Digital Processing, fourth ed. Upper Saddle River, New Jersey: US: Prentice Hall, 2007, pp 496-500.
-
H. M. Hang, Handbook of Visual Communications, first ed. New York: Academic Press, 1995.
-
K. Sayood, Introduction to Data Compression, fifth ed. Cambridge, US: Morgan Kaufmann Publishers, 2018, pp 428-430
Trabajos: 🔗
-
CCITT, “T.81 – Digital Compression and Coding of Continous-Tone Still Images – Requirements and Guidelines", 1992. Disponible: www.w3.org [Accedido: 3/12/2021]
-
K. Cabeen and P. Gent, “Image Compression and the Discrete Cosine Transform". Disponible: www.math.cuhk.edu.hk [Accedido: 3/12/2021]
-
M.R. Azimi, “Digital Image Processing Lectures 11 & 12", presentados Departamento de Ingeniería Eléctrica y Computacional, Colorado State University. [PowerPoint Slides]. Disponible: www.engr.colostate.edu [Accedido: 3/12/2021]
-
CCITT, “T.81 – Digital Compression and Coding of Continous-Tone Still Images – Requirements and Guidelines", 1992. Disponible: www.w3.org [Accedido: 3/12/2021] ↩